Контрольная работа по статитстике

Задание:

Построить интервальный ряд распределения, объединив материал в 8 групп

Вычислить с точностью до 0,1 среднюю арифметическую, моду, медиану, средне – квадратичное отклонение, коэффициент вариации

Изобразить полученный ряд графически при помощи полигона и гистограммы частот (построить 2 графика отдельно)

Определить размах вариации, квартильное отклонение, коэффициент осцилляции, коэффициент линейного отклонения

Определить корреляционное отношение

Решение

1. Построение интервального ряда

Для построения интервального ряда необходимо определить шаг интервала (

i)

I = (

Xmax-

Xmin)/

N

Xmax,

Xmin – максимальное и минимальное значение совокупности

N – Количество образуемых интервалов

I = (7,4

– 5,4

) / 8

= 0,625

№ ряда	Интервал ряда	Частота ряда
1	2,4 – 3,025	10
2	3,025 – 3,65	12
3	3,65 – 4,275	23
4	4,275 – 4,9	15
5	4,9 – 5,525	20
6	5,525 – 6,15	11
7	6,15 – 6,775	7
8	6,775 – 7,4	2
ИТОГО:		100

Вычислить

Среднюю арифметическую

Моду

Медиану

Средне – квадратичное отклонение

Коэффициент вариации

a)

Расчет средней арифметической

Средняя арифметическая в вариационных рядах рассчитывается как средняя арифметическая взвешенная по формуле

Х (средняя) =

Е Х

f /

Е

f, где

Х средняя арифметическая

I - го интервала

f частота ряда

Расчет средней арифметической

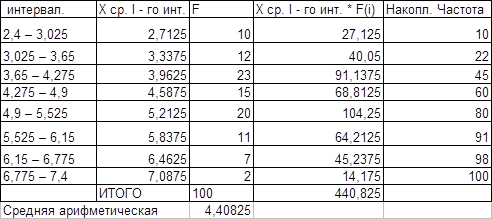
b)

Расчет Моды

Mo = Xo + I * (fmo - fmo-1)/( (fmo - fmo-1) + (fmo - fmo+1)), где

Xo – нижняя граница модального интервала

I – величина интервала

fmo – частота модального интервала

fmo-1 - частота домодального интервала

fmo+1 – частота постмодального интервала

Мода – интервал с большим числом признаков

Mo = 3,65 + 0,625 * (23-12)/((23-12)+(23-15)) = 4,01 тенге

c)

Расчет медианы

Mе =

Xме + Перейти на страницу: 1 2 3 4